Machine Learning — Iris dataset for K-Nearest Neighbors(KNN) Algorithm

Introduction

The K-NN(K-Nearest Neighbor) algorithm is one of simplest yet most used classification algorithm. K-NN is a non-parametric and lazy learning algorithm. It does not learn training data, but instead “memorizes” the training data set. When we want to make a guess, it looks for the closest neighbors in the entire data set.

In the calculation of the algorithm the K value is determined. The meaning of this K value is the number of elements to display. When the value comes, the distance between the value is calculated by taking the nearest K number of elements. The Euclidean function is often used in distance calculation. Manhattan function, Minkowski function and the Hamming function can also be used as the alternatives for Euclidean function. After calculating the distance, classify it and assign the relevant value to the appropriate category.

Iris Dataset

The Iris flower data set or Fisher’s Iris data set is a multivariate data set introduced by the British statistician, eugenicist, and biologist Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis.

The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor).

At the same time, each sample has four properties. These;

• Measuring the length of the sepals in cm
• Measuring the width of the sepals in cm
• Measuring the length of the petals in cm
• Measuring the width of the sepals in cm

Iris flower data set, clustered using k means (left) and true species in the data set (right). Note that k-means is non-determinicstic, so results vary. Cluster means are visualized using larger, semi-transparent markers. The visualization was generated using ELKI

Implementation

We used Euclidean distance as the distance and similarity measure for this sample.

Calculation of Succes:

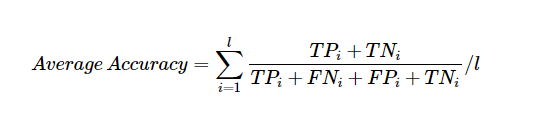
Confusion Matrix:

TP(True Positive) and TN(True Negative) values return the correct number of values

FP(False Positive) and FN(False Negative) values return the wrong number of values

The ratio of the correct value number to all value numbers indicates the correct estimate ratio.

The ratio of the incorrect value number to all value numbers indicates the incorrect estimate ratio.

Confusion matrix result of sample values for Iris data set

Result

The data set showed the best K

For 3 = %95,2380952380952

For 5 = %94,2857142857143

For 10 = %91,4285714285714

And it continued to decrease.

Veysel Guzelsoz.